Egg balance
Egg Balance
imbalance
I often wonder how one would calculate a theoretical optimum way of doing things in daily life. Is it faster to go slowly carrying everything or take two trips going faster? Should I wait for the light, or walk more on this side of the street and cross at the next one? This project came from from that mindset: if there are options, one of them is probably best. I need to determine what “best” is, solve for it, and move on to the next thing.
The video summarizes the little study, and this page has more detail.
This project is a little trivial, but balance is important. Spaceships, satellites, and manipulating things in microgravity requires precise balance and linear and angular inertia calculations. If an automated system is grabbing boxes of things, it’s probably easier if the center of mass isn’t wildly different from one to another.
A chicken egg’s circular shape gives it strength against compressive forces and it has been postulated that its asymmetry evolved to prevent easily rolling away. Neither of these features are especially well suited to protecting eggs in a kitchen-based drop scenario and there is neither the evolutionary motivation nor the time for improvement of the egg itself. Over the course of meals or days, as eggs are removed from opaque paper egg cartons, the center of mass changes. If the center of mass is too far away from the center of geometry, the grasper might, upon first lift, be surprised, unprepared and insufficiently grip the box, dropping the eggs on the floor. Lifting an egg box with one hand requires light touch and if grasp too lightly and in the wrong place, eggs can fall.
This study seeks to identify an optimum sequence of egg removal so someone grasping the box without knowledge of its current configuration will have the best chance of a successful grab by virtue of close alignment of center of mass and center of geometry.
For the purposes of this calculation, the optimum sequence is one in which the average imbalance for all configurations of the box from full to empty is lowest. Standard deviation of the imbalance values for each configuration in a sequence can be used as a second criteria to rank sequences.
The calculation assumes a consistent egg mass, an egg carton mass, and equal spacing between X and Y egg grid locations. As long as those conditions are met, the sequence result should be valid. If the egg mass is consistent but higher or lower in practice, the magnitude of imbalance will be different, but the sequence recommendation would be the same. The same is true for the egg box mass, though if the egg box were infinitely massive, the imbalance would be zero for all egg configurations.
A program was written in Python to calculate the imbalance for each configuration of sequences through 6, 8, 9, and 10-egg boxes. An egg box has two planes of symmetry so for every sequence there are three that are effectively the same, just mirrored. For ease of calculation, half of all possible sequences were used. To calculate the imbalance, the X and Y coordinates for every remaining egg were averaged to give a center of geometry, and multiplied by the mass to give an imbalance vector. That vector was combined with the box mass and centroid to give the total imbalance for the configuration. The program looped through every configuration from full to empty, and looped through every sequence permutation.
All egg boxes had multiple sequences with the same average and only one (four with symmetry) with lowest standard deviation. The graphs below show all of the possible sequences and the imbalances at every configuration.
The optimum sequence for all boxes can be described with the same simple set of guidelines:
1. Corner
2. Exact opposite of the first with respect to the geometric center
3. Furthest egg from the center
4. Exact opposite of (3) with respect to geometric center
5. Back to step 1, taking a corner of whatever is left.
Though removing two more central eggs at the beginning can also start with low imbalance, starting at the corners and working inward allows the mass of the more central eggs to bring the imbalance of any configuration closer to zero. Removing eggs from the outside corners first will reduce angular inertia for easier handling, and if the box is dropped on one end, the remaining eggs have a larger crumple zone to dissipate energy.
So far, I’ve only considered static balance, and there is something to be said for inertial effects and dynamic balancing, but not now.
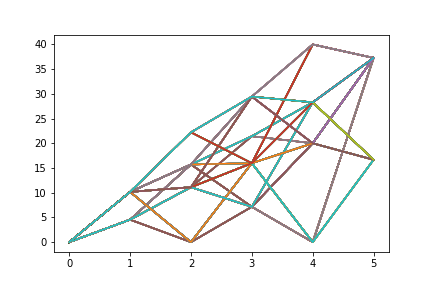
6 Egg Box
X axis: Eggs removed
Y axis: Imbalance, in millimeters distance between center of mass and center of geometry
At zero eggs removed, the box is balanced. In the six egg box, there are two types of eggs to remove: center or corner. The difference in those two can be seen first as the two nodes above 1 on the X axis. With five eggs removed, the remaining egg is either on a corner or center, and those two states are represented by the two nodes above 5 on the X axis.
8 Egg Box
More of the same.
9 Egg Box
In this one, every horizontal line at 0 imbalance represents the situation in which the box is balanced, and the center egg is removed.
10 Egg Box
More of the same.